In-class Exercise 2: Global and Local Measures of Spatial Association - sfdep methods

Author

Cai Jingheng

1 Overview

This in-class introduces an alternative R package to spdep package we used in Chapter 9: Global Measures of Spatial Autocorrelation and Chapter 10: Local Measures of Spatial Autocorrelation. The package is called sfdep. According to Josiah Parry, the developer of the package, “sfdep builds on the great shoulders of spdep package for spatial dependence. sfdep creates an sf and tidyverse friendly interface to the package as well as introduces new functionality that is not present in spdep. sfdep utilizes list columns extensively to make this interface possible.”

2 Getting started

2.1 Installing and Loading the R Packages

Four R packages will be used for this in-class exercise, they are: sf, sfdep, tmap and tidyverse.

Code 
pacman::p_load(sf, sfdep, tmap, tidyverse)

3 The Data

For the purpose of this in-class exercise, the Hunan data sets will be used. There are two data sets in this use case, they are:

  • Hunan, a geospatial data set in ESRI shapefile format, and

  • Hunan_2012, an attribute data set in csv format.

3.1 Importing geospatial data

Code 
hunan <- st_read(dsn = "data/geospatial", 
                 layer = "Hunan")
Reading layer `Hunan' from data source 
  `C:\cjh202311\isss624\In-class_Ex\In-class_Ex2\data\geospatial' 
  using driver `ESRI Shapefile'
Simple feature collection with 88 features and 7 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS:  WGS 84

3.2 Importing attribute table

Code 
hunan2012 <- read_csv("data/aspatial/Hunan_2012.csv")

3.3 Combining both data frame by using left join

Code 
hunan_GDPPC <- left_join(hunan, hunan2012) %>%
  select(1:4, 7, 15)

3.4 Plotting a choropleth map

The choropleth should look similar to the figure below.

Code 
tmap_mode("plot")
tm_shape(hunan_GDPPC) +
  tm_fill("GDPPC", 
          style = "quantile", 
          palette = "Blues",
          title = "GDPPC") +
  tm_layout(main.title = "Distribution of GDP per capita by district, Hunan Province",
            main.title.position = "center",
            main.title.size = 1.2,
            legend.height = 0.45, 
            legend.width = 0.35,
            frame = TRUE) +
  tm_borders(alpha = 0.5) +
  tm_compass(type="8star", size = 2) +
  tm_scale_bar() +
  tm_grid(alpha =0.2)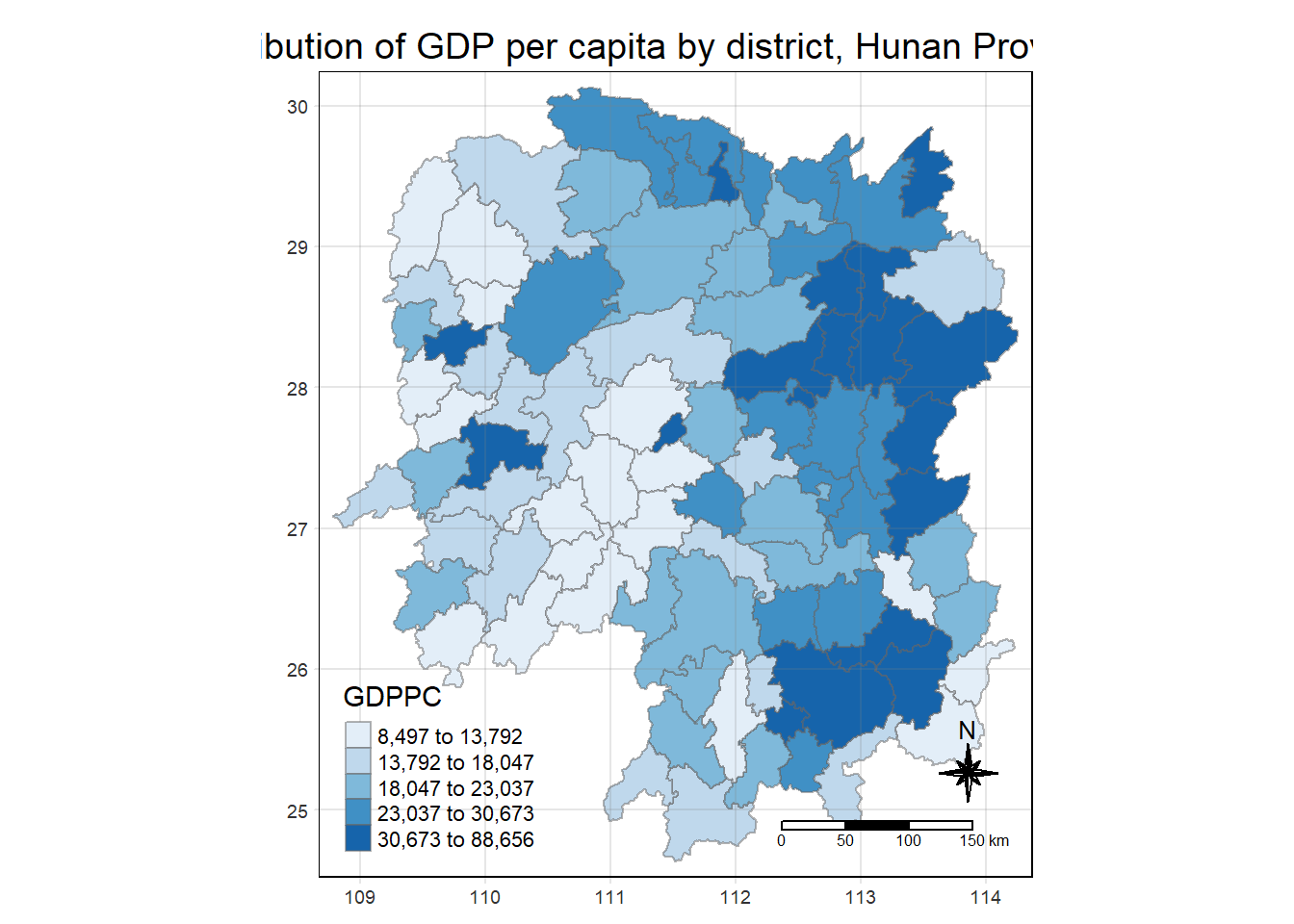

4 Global Measures of Spatial Association

Step 1: Deriving contiguity weights: Queen’s method

Deriving contiguity weights: Queen’s method

In the code chunk below, queen method is used to derive the contiguity weights.

Code 
wm_q <- hunan_GDPPC %>%
  mutate(nb = st_contiguity(geometry),
         wt = st_weights(nb,
                         style = "W"),
         .before = 1)

Notice that st_weights() provides tree arguments, they are:

  • nb: A neighbor list object as created by st_neighbors().

  • style: Default “W” for row standardized weights. This value can also be “B”, “C”, “U”, “minmax”, and “S”. B is the basic binary coding, W is row standardised (sums over all links to n), C is globally standardised (sums over all links to n), U is equal to C divided by the number of neighbours (sums over all links to unity), while S is the variance-stabilizing coding scheme proposed by Tiefelsdorf et al. 1999, p. 167-168 (sums over all links to n).

  • allow_zero: If TRUE, assigns zero as lagged value to zone without neighbors.

Code 
wm_q
Simple feature collection with 88 features and 8 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS:  WGS 84
First 10 features:
                               nb
1                 2, 3, 4, 57, 85
2               1, 57, 58, 78, 85
3                     1, 4, 5, 85
4                      1, 3, 5, 6
5                     3, 4, 6, 85
6                4, 5, 69, 75, 85
7                  67, 71, 74, 84
8       9, 46, 47, 56, 78, 80, 86
9           8, 66, 68, 78, 84, 86
10 16, 17, 19, 20, 22, 70, 72, 73
                                                                            wt
1                                                      0.2, 0.2, 0.2, 0.2, 0.2
2                                                      0.2, 0.2, 0.2, 0.2, 0.2
3                                                       0.25, 0.25, 0.25, 0.25
4                                                       0.25, 0.25, 0.25, 0.25
5                                                       0.25, 0.25, 0.25, 0.25
6                                                      0.2, 0.2, 0.2, 0.2, 0.2
7                                                       0.25, 0.25, 0.25, 0.25
8  0.1428571, 0.1428571, 0.1428571, 0.1428571, 0.1428571, 0.1428571, 0.1428571
9             0.1666667, 0.1666667, 0.1666667, 0.1666667, 0.1666667, 0.1666667
10                      0.125, 0.125, 0.125, 0.125, 0.125, 0.125, 0.125, 0.125
     NAME_2  ID_3    NAME_3   ENGTYPE_3    County GDPPC
1   Changde 21098   Anxiang      County   Anxiang 23667
2   Changde 21100   Hanshou      County   Hanshou 20981
3   Changde 21101    Jinshi County City    Jinshi 34592
4   Changde 21102        Li      County        Li 24473
5   Changde 21103     Linli      County     Linli 25554
6   Changde 21104    Shimen      County    Shimen 27137
7  Changsha 21109   Liuyang County City   Liuyang 63118
8  Changsha 21110 Ningxiang      County Ningxiang 62202
9  Changsha 21111 Wangcheng      County Wangcheng 70666
10 Chenzhou 21112     Anren      County     Anren 12761
                         geometry
1  POLYGON ((112.0625 29.75523...
2  POLYGON ((112.2288 29.11684...
3  POLYGON ((111.8927 29.6013,...
4  POLYGON ((111.3731 29.94649...
5  POLYGON ((111.6324 29.76288...
6  POLYGON ((110.8825 30.11675...
7  POLYGON ((113.9905 28.5682,...
8  POLYGON ((112.7181 28.38299...
9  POLYGON ((112.7914 28.52688...
10 POLYGON ((113.1757 26.82734...

Computing Global Moran’ I

In the code chunk below, global_moran() function is used to compute the Moran’s I value. Different from spdep package, the output is a tibble data.frame.

Code 
moranI <- global_moran(wm_q$GDPPC,
                       wm_q$nb,
                       wm_q$wt)
glimpse(moranI)
List of 2
 $ I: num 0.301
 $ K: num 7.64

Performing Global Moran’sI test

In general, Moran’s I test will be performed instead of just computing the Moran’s I statistics. With sfdep package, Moran’s I test can be performed by using global_moran_test() as shown in the code chunk below.

Code 
global_moran_test(wm_q$GDPPC,
                       wm_q$nb,
                       wm_q$wt)

    Moran I test under randomisation

data:  x  
weights: listw    

Moran I statistic standard deviate = 4.7351, p-value = 1.095e-06
alternative hypothesis: greater
sample estimates:
Moran I statistic       Expectation          Variance 
      0.300749970      -0.011494253       0.004348351

Performing Global Moran’I permutation test

In practice, monte carlo simulation should be used to perform the statistical test. For sfdep, it is supported by globel_moran_perm()

It is always a good practice to use set.seed() before performing simulation. This is to ensure that the computation is reproducible.

Code 
set.seed(1234)

Next, global_moran_perm() is used to perform Monte Carlo simulation.

Code 
global_moran_perm(wm_q$GDPPC,
                       wm_q$nb,
                       wm_q$wt,
                  nsim = 99)

    Monte-Carlo simulation of Moran I

data:  x 
weights: listw  
number of simulations + 1: 100 

statistic = 0.30075, observed rank = 100, p-value < 2.2e-16
alternative hypothesis: two.sided

The report above show that the p-value is smaller than alpha value of 0.05. Hence, reject the null hypothesis that the spatial patterns spatial independent. Because the Moran’s I statistics is greater than 0. We can infer the spatial distribution shows sign of clustering.

5 Computing local Moran’s I

In this section, we will learn how to compute Local Moran’s I of GDPPC at county level by using local_moran() of sfdep package.

Code 
lisa <- wm_q %>% 
  mutate(local_moran = local_moran(
    GDPPC, nb, wt, nsim = 99),
         .before = 1) %>%
  unnest(local_moran)

The output of local_moran() is a sf data.frame containing the columns ii, eii, var_ii, z_ii, p_ii, p_ii_sim, and p_folded_sim.

  • ii: local moran statistic

  • eii: expectation of local moran statistic; for localmoran_permthe permutation sample means

  • var_ii: variance of local moran statistic; for localmoran_permthe permutation sample standard deviations

  • z_ii: standard deviate of local moran statistic; for localmoran_perm based on permutation sample means and standard deviations

  • p_ii: p-value of local moran statistic using pnorm(); for localmoran_perm using standard deviatse based on permutation sample means and standard deviations

  • p_ii_sim: For localmoran_perm(), rank() and punif() of observed statistic rank for [0, 1] p-values using alternative=

  • p_folded_sim: the simulation folded [0, 0.5] range ranked p-value based on crand.py of pysal

  • skewness: For localmoran_perm, the output of e1071::skewness() for the permutation samples underlying the standard deviates

  • kurtosis: For localmoran_perm, the output of e1071::kurtosis() for the permutation samples underlying the standard deviates.

Visualising local Moran’s I

In this code chunk below, tmap functions are used prepare a choropleth map by using value in the ii field.

Code 
tmap_mode("plot")
tm_shape(lisa) +
  tm_fill("ii") + 
  tm_borders(alpha = 0.5) +
  tm_view(set.zoom.limits = c(6,8)) +
  tm_layout(main.title = "local Moran's I of GDPPC",
            main.title.size = 0.8)

Visualising p-value of local Moran’s I

In the code chunk below, tmap functions are used prepare a choropleth map by using value in the p_ii_sim field.

Code 
tmap_mode("plot")
tm_shape(lisa) +
  tm_fill("p_ii_sim") + 
  tm_borders(alpha = 0.5) +
   tm_layout(main.title = "p-value of local Moran's I",
            main.title.size = 0.8)

Visualising local Moran’s I and p-value

For effective comparison, it will be better for us to plot both maps next to each other as shown below.

Code 
tmap_mode("plot")
map1 <- tm_shape(lisa) +
  tm_fill("ii") + 
  tm_borders(alpha = 0.5) +
  tm_view(set.zoom.limits = c(6,8)) +
  tm_layout(main.title = "local Moran's I of GDPPC",
            main.title.size = 0.8)

map2 <- tm_shape(lisa) +
  tm_fill("p_ii_sim",
          breaks = c(0, 0.001, 0.01, 0.05, 1),
              labels = c("0.001", "0.01", "0.05", "Not sig")) + 
  tm_borders(alpha = 0.5) +
  tm_layout(main.title = "p-value of local Moran's I",
            main.title.size = 0.8)

tmap_arrange(map1, map2, ncol = 2)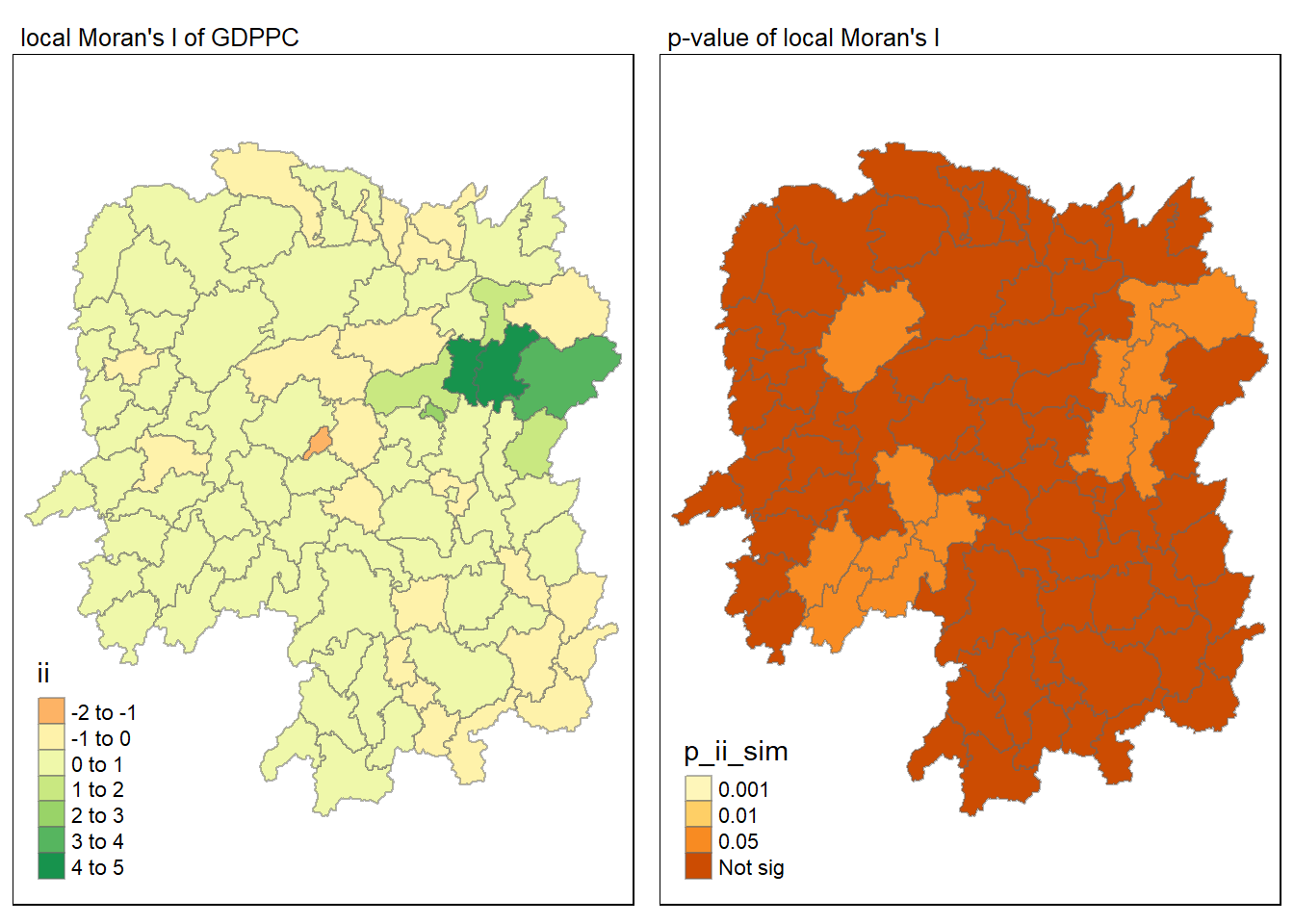

Visualising LISA map

LISA map is a categorical map showing outliers and clusters. There are two types of outliers namely: High-Low and Low-High outliers. Likewise, there are two type of clusters namely: High-High and Low-Low cluaters. In fact, LISA map is an interpreted map by combining local Moran’s I of geographical areas and their respective p-values.

In lisa sf data.frame, we can find three fields contain the LISA categories. They are mean, median and pysal. In general, classification in mean will be used as shown in the code chunk below.

Code 
lisa_sig <- lisa  %>%
  filter(p_ii_sim < 0.05)
tmap_mode("plot")
tm_shape(lisa) +
  tm_polygons() +
  tm_borders(alpha = 0.5) +
tm_shape(lisa_sig) +
  tm_fill("mean") + 
  tm_borders(alpha = 0.4)

6 Hot Spot and Cold Spot Area Analysis (HCSA)

HCSA uses spatial weights to identify locations of statistically significant hot spots and cold spots in an spatially weighted attribute that are in proximity to one another based on a calculated distance. The analysis groups features when similar high (hot) or low (cold) values are found in a cluster. The polygon features usually represent administration boundaries or a custom grid structure.

7 Computing local Gi* statistics

Code 
wm_idw <- hunan_GDPPC %>%
  mutate(nb = st_contiguity(geometry),
         wts = st_inverse_distance(nb, geometry,
                                   scale = 1,
                                   alpha = 1),
         .before = 1)

Next, local_gstar_perm() of sfdep package will be used to compute local Gi* statistics as shown in the code chunk below.

Code 
HCSA <- wm_idw %>% 
  mutate(local_Gi = local_gstar_perm(
    GDPPC, nb, wt, nsim = 499),
         .before = 1) %>%
  unnest(local_Gi)
HCSA
Simple feature collection with 88 features and 16 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS:  WGS 84
# A tibble: 88 × 17
   gi_star   e_gi    var_gi p_value   p_sim p_folded_sim skewness kurtosis nb   
     <dbl>  <dbl>     <dbl>   <dbl>   <dbl>        <dbl>    <dbl>    <dbl> <nb> 
 1  0.0416 0.0114   6.24e-6  0.0472 9.62e-1        0.84     0.42     0.739 <int>
 2 -0.333  0.0112   6.39e-6 -0.301  7.64e-1        0.932    0.466    0.852 <int>
 3  0.281  0.0125   7.83e-6 -0.0911 9.27e-1        0.872    0.436    1.01  <int>
 4  0.411  0.0113   7.14e-6  0.508  6.11e-1        0.568    0.284    0.868 <int>
 5  0.387  0.0114   7.81e-6  0.421  6.74e-1        0.54     0.27     1.25  <int>
 6 -0.368  0.0116   6.81e-6 -0.478  6.33e-1        0.764    0.382    0.914 <int>
 7  3.56   0.0146   7.04e-6  2.84   4.56e-3        0.032    0.016    1.09  <int>
 8  2.52   0.0135   5.08e-6  1.69   9.14e-2        0.148    0.074    0.797 <int>
 9  4.56   0.0141   4.57e-6  4.12   3.71e-5        0.008    0.004    1.03  <int>
10  1.16   0.0109   4.92e-6  1.35   1.76e-1        0.208    0.104    0.597 <int>
# ℹ 78 more rows
# ℹ 8 more variables: wts <list>, NAME_2 <chr>, ID_3 <int>, NAME_3 <chr>,
#   ENGTYPE_3 <chr>, County <chr>, GDPPC <dbl>, geometry <POLYGON [°]>

Visualising Gi*

Code 
tmap_mode("plot")
tm_shape(HCSA) +
  tm_fill("gi_star") + 
  tm_borders(alpha = 0.5) +
  tm_view(set.zoom.limits = c(6,8))

Visualising p-value of HCSA

Code 
tmap_mode("plot")
tm_shape(HCSA) +
  tm_fill("p_sim") + 
  tm_borders(alpha = 0.5)

Visuaising local HCSA

For effective comparison, we can plot both maps next to each other as shown below.

Code 
tmap_mode("plot")
map1 <- tm_shape(HCSA) +
  tm_fill("gi_star") + 
  tm_borders(alpha = 0.5) +
  tm_view(set.zoom.limits = c(6,8)) +
  tm_layout(main.title = "Gi* of GDPPC",
            main.title.size = 0.8)

map2 <- tm_shape(HCSA) +
  tm_fill("p_sim",
          breaks = c(0, 0.001, 0.01, 0.05, 1),
          labels = c("0.001", "0.01", "0.05", "Not sig")) + 
  tm_borders(alpha = 0.5) +
  tm_layout(main.title = "p-value of Gi*",
            main.title.size = 0.8)

tmap_arrange(map1, map2, ncol = 2)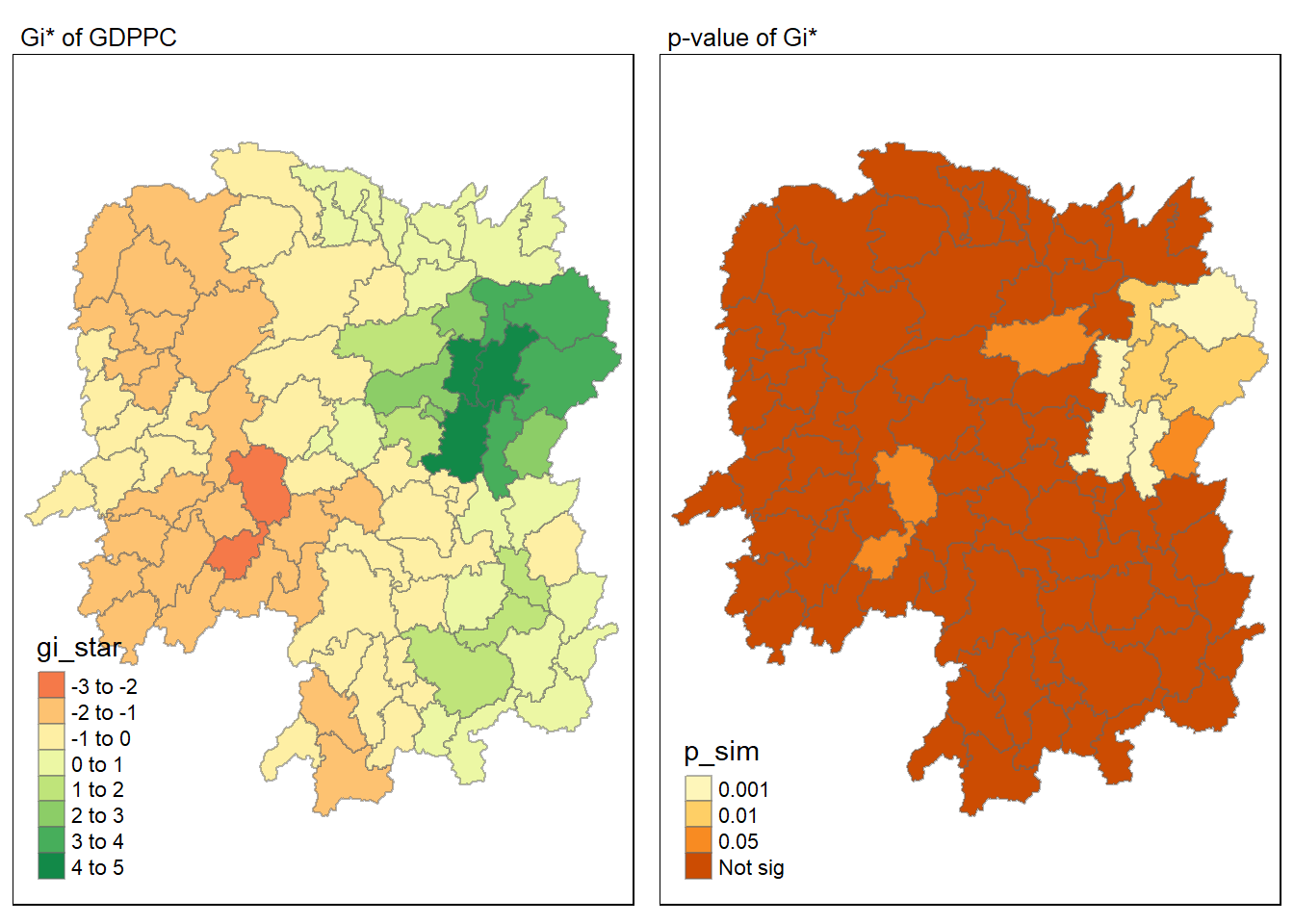

8 Visualising hot spot and cold spot areas

Now, we are ready to plot the significant (i.e. p-values less than 0.05) hot spot and cold spot areas by using appropriate tmap functions as shown below.

Code 
HCSA_sig <- HCSA  %>%
  filter(p_sim < 0.05)
tmap_mode("plot")
tm_shape(HCSA) +
  tm_polygons() +
  tm_borders(alpha = 0.5) +
tm_shape(HCSA_sig) +
  tm_fill("gi_star") + 
  tm_borders(alpha = 0.4)

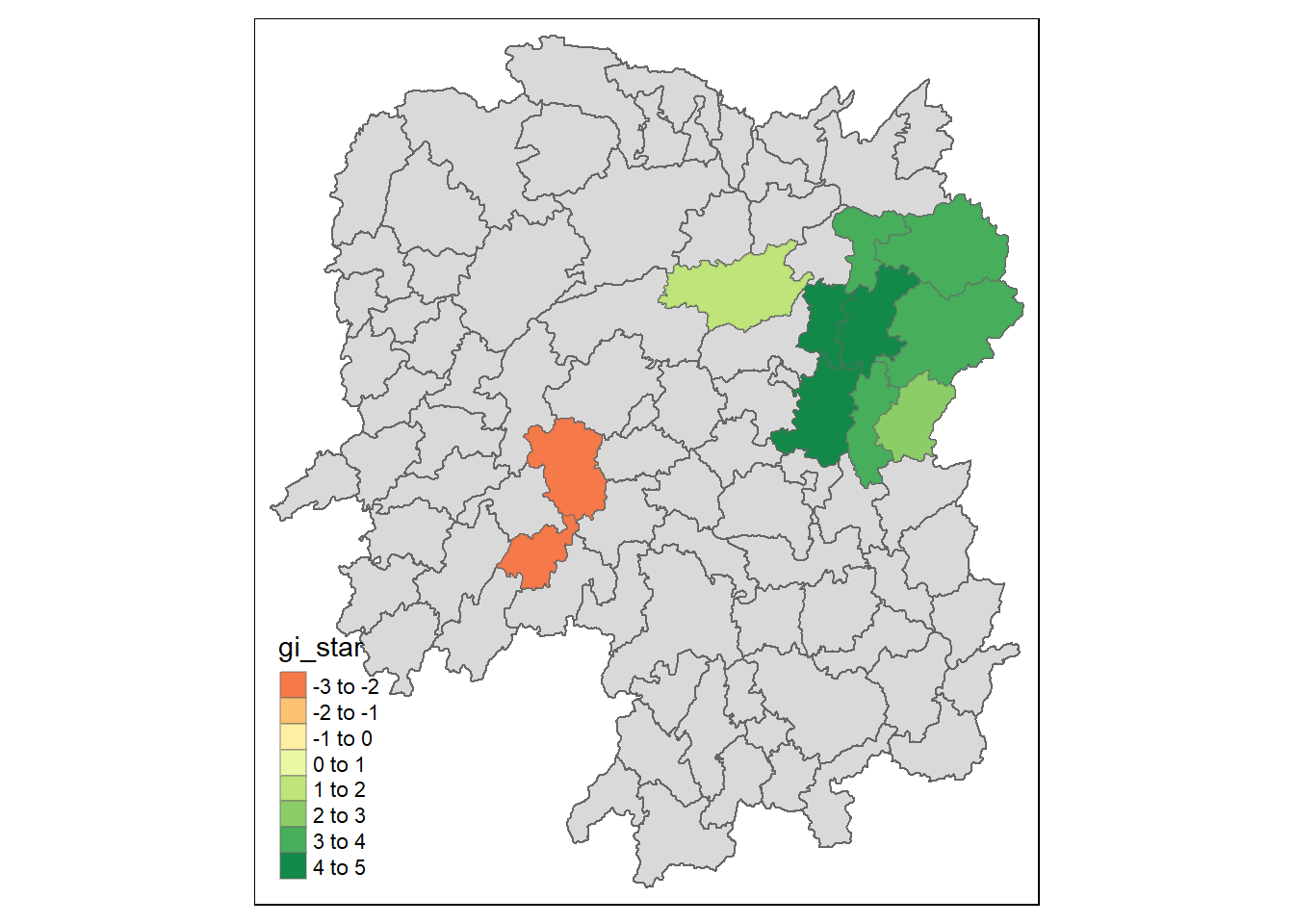
Figure above reveals that there is one hot spot area and two cold spot areas. Interestingly, the hot spot areas coincide with the High-high cluster identifies by using local Moran’s I method in the earlier sub-section.